A maioria das pessoas tem uma noção intuitiva de o que é risco. Em linhas gerais, risco é exposição a um perigo. Todos corremos riscos. E nem sempre somos completamente racionais quanto a isso no nosso dia a dia.

Por Gabriel Koike

O que é risco

Em uma leitura mais detalhada, exposição a um perigo tem duas componentes fundamentais. A exposição é a chance – probabilidade – de algum perigo se concretizar. O perigo é a severidade das consequências, caso essa chance se concretize. Com essa visão, há toda uma ciência que se pode expandir em diversas direções. Essa visão dual – probabilidade e severidade – é o conceito base para se entender risco e segurança desde produtos como carros, aviões e até usinas nucleares, e contratos e serviços como seguros, taxas de juros e investimentos.

Para o caso de investimentos, podemos pensar que é uma razão entre possibilidade de perdas e probabilidades associadas a essas perdas. Por exemplo, “qual a probabilidade de se ter uma perda de x% do valor de meu portfólio em um dia?”, ou – indo em direção ao conceito de Value-at-Risk (VaR), “Qual o valor relativo ao meu portfólio, tal que com probabilidade y%, meu resultado diário será melhor que este valor?”.

Na verdade, um dos passos principais para se entender risco é formular estas perguntas – porque a forma como as perguntas são feitas determina o tipo de resposta – e consequentemente o modelamento matemático do problema.

Desenvolvida a intuição, pode-se pensar em formas de quantificar risco. Para isso, emprestamos da matemática a Teoria de Probabilidade – variáveis aleatórias, processos estocásticos, distribuições de probabilidade – e de Estatística.

Fazendo as Perguntas Certas

Para definir Value-At-Risk de forma mais precisa, é necessário explorar as perguntas certas quanto a risco. Na verdade, há vários “sabores” de Value-At-Risk. Cada um respondendo a uma pergunta formulada de um jeito. E para cada uma das perguntas pode haver mais de uma resposta, tudo dependendo das premissas.

A pergunta clássica do Value-At-Risk é: “Qual o valor do meu portfólio que eu posso perder, com 5% de probabilidade, em um dia?”. O valor de 5%, e o horizonte de tempo de 1 dia são alguns dos números mais clássicos – e os que exploraremos, apesar de ser facilmente extensível para outros valores de probabilidade de tempo. É esta pergunta que vamos considerar quando falamos de Value-At-Risk neste artigo.

Entre outras perguntas que formulam diferentes aproximações ao Value-At-Risk­, encontramos também: “Com o portfólio que tenho hoje, qual seria a pior perda histórica em um dia, considerando os retornos históricos dos ativos?”. Esta formulação é também conhecida como “VaR Histórico”. Uma das grandes limitações para nós, em um fundo sistemático, de pensarmos nesta pergunta é: como operamos de forma sistemática, faz sentido considerarmos que teríamos este mesmo portfólio durante toda a história considerada, para que tivéssemos esta perda máxima?

Há também o Conditional Value-At-Risk, ou Expected Shortfall, que é um valor um pouco mais conservador do que a estimativa clássica. “Qual o valor esperado de uma perda diária em meu portfólio, caso esteja em um dos 5% piores retornos esperados?”. A nuance é a parte condicional da segunda parte da frase. Ela já parte da premissa que se está em um dia excepcionalmente ruim, então a partir daí tenta determinar o valor de uma perda esperada. Para vários modelos matemáticos, esta pergunta é quase equivalente à primeira, mas isso depende de uma série de hipóteses que não necessariamente são estritamente verdadeiras.

Riscos e Volatilidade

Há várias formas de se pensar em riscos de um portfólio. Talvez o risco mais óbvio seja o risco de flutuações indesejadas de preço: um comprador de um ativo espera que este se valorize com o tempo – mas preços se comportam, no tempo, de uma forma não puramente determinística. É nesse tipo de risco e características de oscilações nos retornos que estaremos interessados nessa abordagem do Value-At-Risk.

Escrevemos sobre este tipo de flutuações e características de retornos no nosso artigo de volatilidade. Este artigo se apoia em alguns conceitos de artigos anteriores, então não exploraremos a fundo estes conceitos.

O objetivo primário é desenvolver a intuição sobre o assunto, então vamos começar de um caso simples e gradativamente aumentar a complexidade. Consideremos, incialmente, um portfólio composto por apenas um ativo A. O ativo A tem uma volatilidade denotada por σ_A.

A volatilidade do ativo é uma característica estimada de um modelo de comportamento estatístico, que reflete variações esperadas deste ativo no decorrer do tempo. Em particular, a volatilidade é a raiz quadrada da variância – o segundo momento do retorno (valor esperado do retorno centralizado ao quadrado). Ou seja, a volatilidade nos dá uma métrica de “quanto” oscilações do preço são esperadas. Quanto maior a volatilidade, maiores as oscilações esperadas.

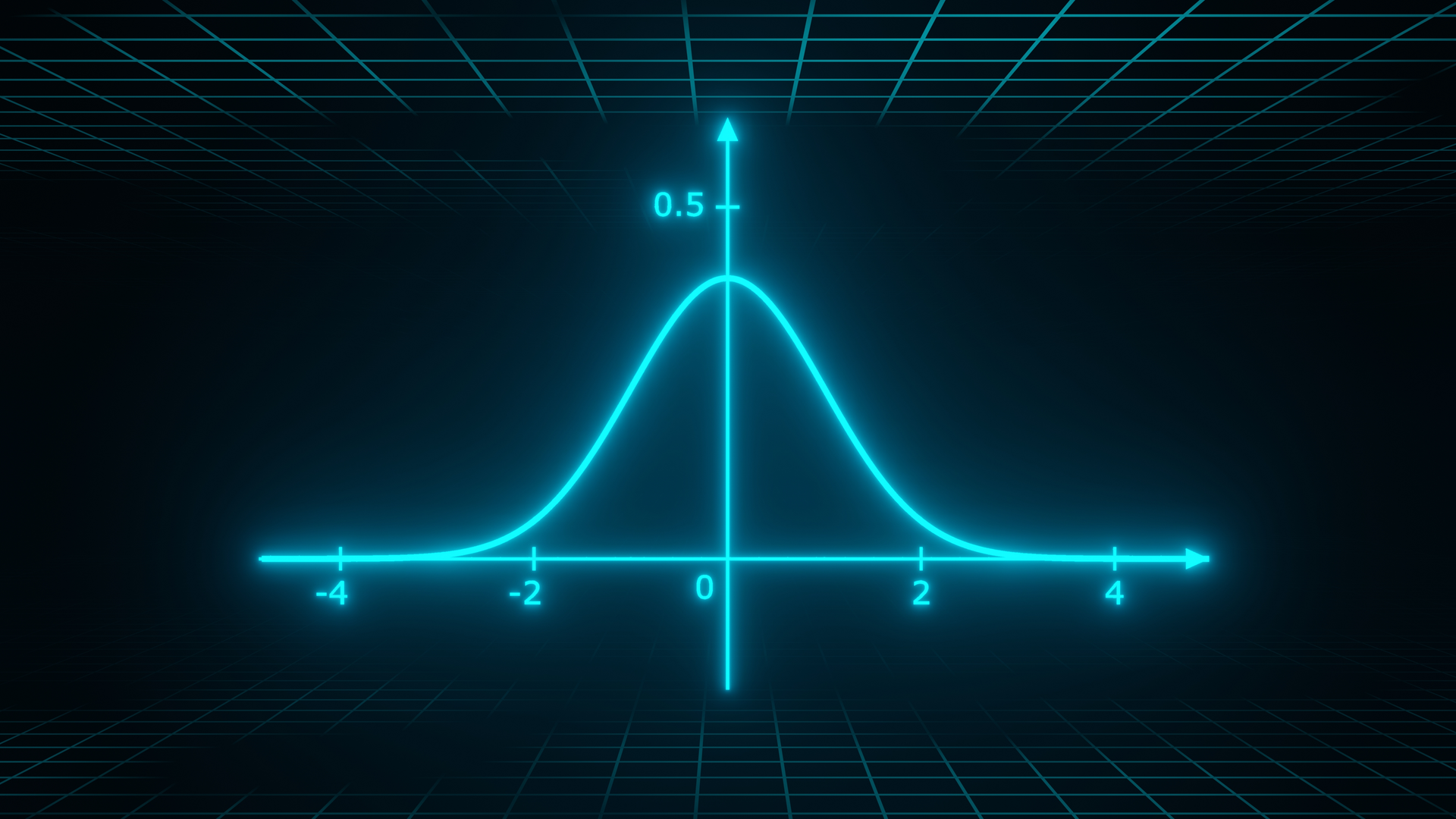
Para responder à pergunta de Value-at-Risk deste portfólio de forma quantitativa, no entanto, precisamos de mais uma hipótese: sobre a distribuição dos retornos. A distribuição é a característica de uma variável aleatória que amarra intervalos de valores a probabilidades, com uma descrição matemática. Uma hipótese simplista (e não realista) é a de distribuição Gaussiana, ou Normal. Distribuições Gaussianas são muito comummente encontradas em outros campos, como em fenômenos físicos ou biológicos, e em diversos outros campos, frequentemente como consequência do Teorema do Limite Central. Uma fraqueza desta hipótese é que, comparada a retornos típicos de mercado, a distribuição Gaussiana tende a subestimar a probabilidade de movimentos de grande amplitude. Há diversos tipos de ajustes a se fazer sobre este tipo de hipótese, mas em benefício da simplicidade de explicação e intuição, seguiremos com ela.

A distribuição dos retornos nos permite quantificar, conhecida a volatilidade, a probabilidade de retornos versus a amplitude de movimentos. No nosso exemplo, estamos interessados no valor limite do intervalo inferior da distribuição equivalente a uma probabilidade de 5%. Para o caso de uma distribuição Gaussiana, isso é aproximadamente 1.65σ, sendo σ a raiz quadrada da variância.

Numericamente, suponhamos que o ativo A tem volatilidade anualizada de 20%. Nesse caso, a volatilidade diarizada (estamos interessados na possibilidade de perda em um dia) seria aproximadamente 1.26%, então o VaR seria de aproximadamente 2.08% do portfólio. Ou seja, se o portfólio tivesse um tamanho de 100,000.00 reais, o Value-at-Risk de 5% em um dia – o valor que pode se esperar perder em um dia com uma probabilidade de 5% é de 2078.05 reais.

Covariância e Diversificação

Entendido o exemplo simples, vou estender a análise para dois ativos – progrediremos aos poucos. Vamos supor então que nosso portfolio agora é composto por dois ativos, A e B. Em particular, nosso portfólio terá uma proporção w_A do ativo A, e w_B do ativo B e estes ativos, por sua vez, têm volatilidades σ_A e σ_B. Com dois ativos, teremos um efeito mais interessante. Se pensássemos no Value-at-Risk como no portfólio simplificado, seria intuitivo pensar que, com as quantidades do portfólio, teríamos um Value-at-Risk de 1.65w_A σ_A oriundo da nossa exposição a A, e 1.65w_B σ_B de nossa exposição a B.

Mas essa abordagem pode ter um problema ao ser excessivamente conservadora: se somássemos os VaR de A e B, estaríamos considerando um caso especial em que a perda ocorre tanto no ativo A quanto no ativo B simultaneamente. Embora isso seja possível, essas perdas relativas a uma probabilidade de 5% acontecerem simultaneamente e a probabilidade se manter a mesma exige uma hipótese forte: que os ativos A e B são perfeitamente correlacionados – ou seja, se o preço de A sobe, o preço de B também sobe em mesma intensidade. Nesse caso, não seria lá muito vantajoso investir tanto em A quanto em B, dado que são equivalentes.

O que deve considerar, então, é a covariância entre estes dois ativos. Ou seja, a proporção esperada entre variações de preços dos ativos A e B. Por exemplo, se A e B forem ações de empresas de um mesmo setor e de porte parecido, pode-se esperar que tenham uma certa correlação. Da mesma forma, se forem empresas muito diferentes, em diferentes regiões geográficas, setores diferentes, é possível que tenham pouca correlação entre si.

Devemos, então, passar a pensar na variância do portfólio como um todo, e não apenas nas variâncias ou volatilidades de A e B separadamente. O leitor mais atento pode começar a uma implicação bastante direta desse tipo de pensamento: diversificação. Em termos matemáticos, a variância do portfólio será dada por:

Onde Cov(A,B) é a covariância de A e B. A covariância mínima ocorre quando A e B se movem em oposição máxima. Por exemplo, se A = -xB (ou seja, comprar uma unidade de A equivale a vender x unidades de B). A covariância máxima ocorre quando A e B se movem em perfeita sincronia. Evidentemente que nenhum desses extremos é desejado, em geral (apesar de conceitos parecidos serem úteis em situações especiais, mas que não são o foco desta discussão) – afinal de contas, a primeira opção seria contraprodutiva pois um ativo “tira” o lucro esperado de outro e na segunda opção não há diversificação alguma – seria mais simples usar um único ativo para montar o portfólio.

Agora uma coisa interessante a se observar na matemática da discussão. Quando os ativos são perfeitamente correlacionados, temos:

Que é o resultado intuitivo que tivemos antes de começar a falar de covariâncias. E como isso ocorre quando os ativos são perfeitamente correlacionados, então temos que se A e B não forem perfeitamente correlacionados, necessariamente:

Ou seja, quando os ativos A e B são descorrelacionados – o portfólio é diversificado, teremos que o risco esperado do portfólio é menor do que teríamos caso os ativos fossem perfeitamente correlacionados, ou de um portfólio não-diversificado.

Entendida a discussão em 2 ativos, podemos então generalizar para n ativos. A intuição é a mesma. Sem precisar entrar em detalhes da matemática, temos que:

Sendo que Cov(i,j) são as covariâncias entre os ativos i e j, e a covariância entre i e i é a própria variância do ativo i. Descoberta a variância do portfólio, a conta para o VaR é a mesma – dependente da premissa da distribuição – e vale 1.65 para uma distribuição Gaussiana, considerando perdas com 5% de probabilidade.

Value-at-Risk no mundo real

Conceitos de Value-at-Risk são muito usados como métrica de risco de portfólios. Como vimos, o cálculo do VaR leva em conta a diversificação do portfólio e consolidam esse tipo de informação de forma muito elegante – ter uma métrica única que sintetiza o risco como formulado é realmente conveniente. Dito isso, o VaR possui limitações.

Como discutimos, o VaR é apenas uma resposta a uma pergunta bastante específica. Formular perguntas diferentes sobre risco nos dará respostas diferentes sobre outros aspectos de risco, então não há exatamente uma única resposta sobre “risco” – na realidade há muitos outros aspectos a ser considerados.

Além disso, há uma série de premissas e informações necessárias para estimar o VaR. Na nossa discussão, explicitamos a hipótese de distribuição Gaussiana. Esta hipótese é conhecidamente falsa para retornos financeiros. É um modelo, e um modelo reconhecidamente limitado. Não apenas isso, mas a limitação deste modelo se dá exatamente nos extremos – exatamente onde gostaríamos de ter uma estimativa melhor, dada a formulação de nossa pergunta do VaR.

Também supusemos conhecidas as variâncias e covariâncias. No mundo real, é algo bastante difícil de estimar (e facilmente tema de artigos mais técnicos), e estas coisas não necessariamente se comportam de forma estática. Por exemplo, em crises como COVID-19, diversos ativos tipicamente pouco correlacionados se comportaram de forma correlacionada e tiveram quedas bruscas de grande amplitude e ao mesmo tempo, pois na verdade houve um risco sistêmico que se concretizou.

Estas ressalvas não descartam a utilidade do Value-at-Risk. Mas conhecer as características, as limitações, as hipóteses e a mecânica por trás do modelo nos permitem extrair o máximo de cada uma de nossas ferramentas.