Um texto sobre como uma relação estatística entre as trajetórias de um cachorro e seu dono pode ser aplicada em estratégias de investimento.
Por Hully Rolemberg
Você muito provavelmente já ouviu falar de “correlação” e sabe formular uma definição intuitiva sobre esse conceito: correlação significa uma relação entre duas coisas. O fato é que existe um “refinamento” da ideia de correlação que nos permite avaliar relações de longo prazo e obter insights mais profundos sobre o comportamento conjunto de duas variáveis, é o que chamamos de cointegração.
Por trás da definição de cointegração, há uma extensa literatura estatística sobre estacionariedade, raízes unitárias, modelos autorregressivos etc. Mas, como o meu objetivo nunca é te entediar com fórmulas matemáticas e explicações rebuscadas, hoje vou pular alguns passos e te explicar o que é cointegração usando uma adaptação de Murray (1994) sobre o bêbado e o cachorro.
Inicialmente, imagine um bêbado que acaba de sair do bar, ele caminha em uma rua plana tentando chegar em casa. Toda vez que o bêbado caminha para frente, ele pode tombar para esquerda ou para a direita com probabilidades iguais. Dizemos então que a trajetória dele segue um “passeio aleatório”, ou seja, é uma sucessão de passos aleatórios.
Bêbados não são os únicos com comportamentos desse tipo, cães também podem agir assim: cada cheiro que passa aleatoriamente pelo nariz do cachorro determina a direção do seu próximo passo. Com isso em mente, suponha que um cachorro (que a princípio não pertence ao bêbado) saia do bar no mesmo instante que o bêbado. As trajetórias do bêbado (𝑥) e do cachorro (𝑦) podem ser modeladas da seguinte forma:
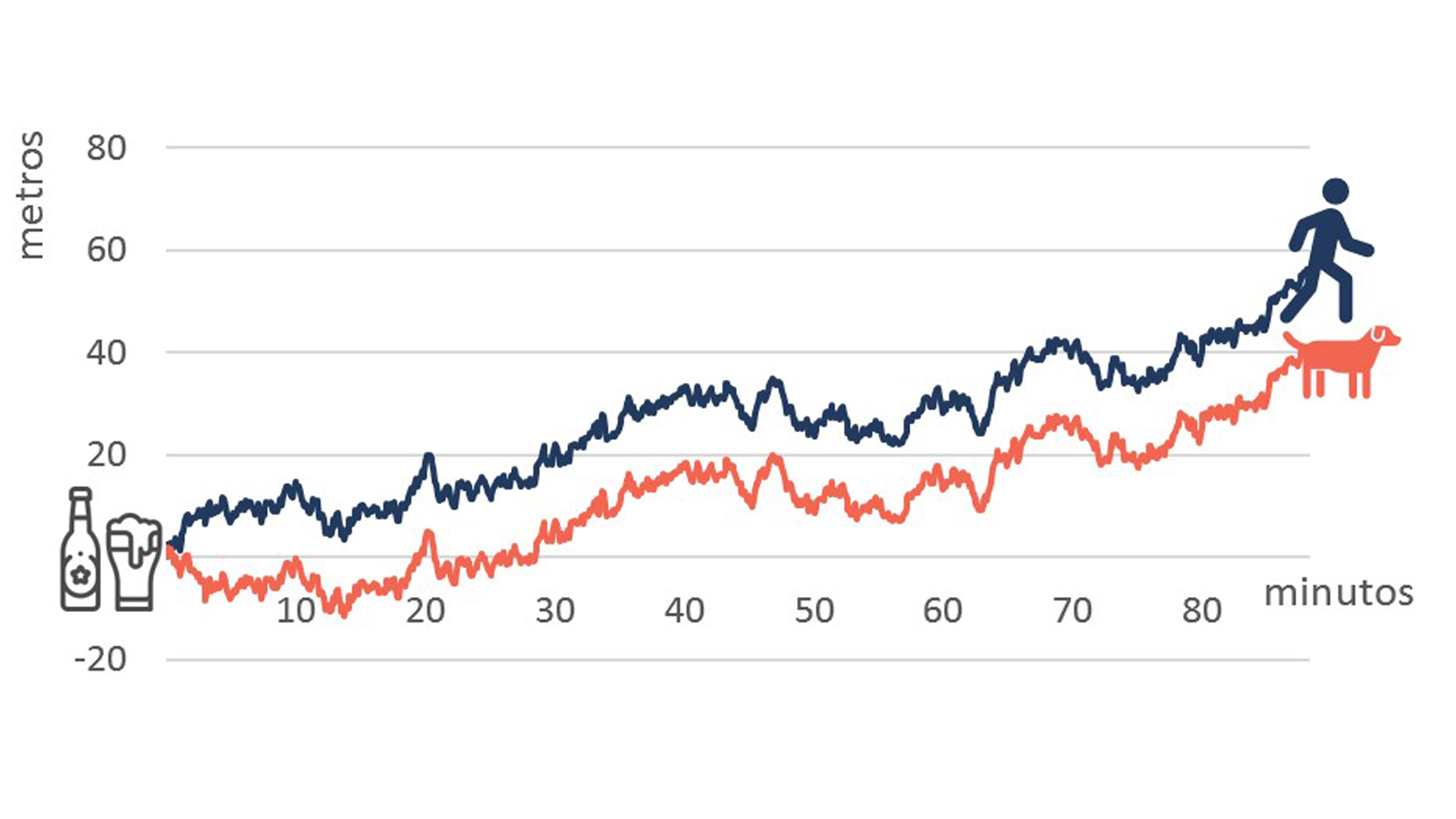
onde ut e wt são os passos aleatórios que o bêbado e o cachorro dão no instante t. Esses passos seguem, por hipótese, um processo estocástico do tipo ruído branco, isto é, estacionário e não autocorrelacionado. Graficamente, podemos ilustrar essa situação da seguinte forma: o eixo horizontal representa o tempo e o eixo vertical a localização, de forma que o bar está localizado no ponto zero do eixo vertical (veja a figura abaixo).
Uma característica importante de processos do tipo passeio aleatório é que o último valor observado é a melhor previsão para os valores futuros. Isso ocorre porque o próximo ponto é exatamente o anterior mais um erro aleatório. Sendo assim, se me perguntassem onde estão o bêbado e o cachorro agora, a minha melhor resposta seria dizer que eles estão no último lugar onde eu os vi: no bar.
Observe que, como passeios aleatórios são processos não-estacionários (integrados de ordem 1), quanto mais tempo passa, maiores são as chances de o bêbado e o cachorro estarem longe de onde eles foram vistos pela última vez (no bar) e, além disso, maiores as chances de estarem distantes um do outro. Mas, e se o cão pertencer ao bêbado?
Suponha então que o cão pertence ao bêbado. O bêbado e o cachorro saem do bar e seguem (individualmente) passeios aleatórios, mas eventualmente o dono chama o cão: “Ethos!”. O cão entende que não pode se afastar demais do dono senão ficará trancado para fora de casa, e o bêbado entende que não pode deixar o cão ir muito longe senão vai acordar com o seu latido do lado de fora de casa. Sendo assim, tanto o cão quanto o bêbado passam a caminhar de forma a não se afastarem demais, sempre corrigindo a distância entre eles. Agora, as trajetórias do bêbado e do cão não seguem mais processos do tipo passeio aleatório, pois incluem um termo de correção de erro que impede que os dois se afastem demais um do outro. Uma possível representação gráfica, nesse caso, seria a seguinte:
Observe que tanto o cão quanto o dono continuam dando passos aleatórios para esquerda e para a direita ao longo do caminho e, conforme o tempo passa, a probabilidade de eles estarem longe do bar cresce. Ou seja, apesar de as novas trajetórias não seguirem (conjuntamente) processos do tipo passeio aleatório, elas ainda são não-estacionárias.
Sabendo que o cão pertence ao bêbado, nosso melhor chute agora é dizer que uma vez encontrado o bêbado, o cão não deve estar muito longe (e vice-versa). Se isso for verdade, então a distância entre as duas trajetórias é estacionária e a caminhada do bêbado e do cachorro são cointegradas de ordem zero (essa definição será explicada a seguir).
Lembre-se de que o cão não está preso a uma coleira que o força a estar uma distância fixa de seu dono. A distância entre ele e o bêbado é, na verdade, uma variável aleatória estacionária, apesar da não-estacionariedade das trajetórias. Uma pausa para algumas explicações teóricas. Processos não-estacionários que se tornam estacionários quando diferenciado n vezes são chamados “integrados de ordem n”. Para que um conjunto de séries “cointegre”, é necessário que todas as séries sejam integradas da mesma ordem e que exista uma combinação linear (com pesos não nulos) entre elas tal que o resultado seja integrado de ordem menor que a das séries originais.
Intuitivamente, cointegração é um conceito probabilístico que define uma relação de longo prazo entre duas variáveis. Nós podemos modelar as trajetórias cointegradas do bêbado e de seu cachorro da seguinte forma:
onde ut e wt continuam sendo os passos do bêbado e do cão. O segundo termo do lado direito de cada equação é o termo de correção de erro segundo o qual o cachorro e o bêbado provavelmente não vão se afastar muito um do outro. Do sistema acima, deduzimos que a relação de cointegração entre y e x é (xt-1 – yt-1).
Note que se os termos de correção de erro não fossem estacionários, então os passos do bêbado e do seu cachorro também não seriam estacionários e então eles caminhariam para longe um do outro mesmo que se esforçassem para ficarem juntos. Sendo assim, se o bêbado e seu cão seguem trajetórias integradas de ordem 1 e consistentes com o sistema de equações descrito anteriormente, então as trajetórias devem cointegrar.
Mesmo valores pequenos de (c+d) têm efeitos significativos em reduzir a distância entre o bêbado e seu cachorro. Os dois tentam balancear os seus passos dados os passos do outro, de forma que a soma das suas posições seja uma variável estacionária com média zero. Imagine que o bêbado e o cachorro não consigam balancear perfeitamente os seus passos, um deve ser mais pesado que o outro e isso afeta o tamanho do passo, por exemplo. Nesse caso, a variável estacionária seria a média ponderada das posições do homem e do cachorro.
Quando utilizamos variáveis não-estacionárias em modelos de regressão convencionais, podemos obter resultados enganosos. Isto é, como processos do tipo passeio aleatório são não estacionários, se quiséssemos usar a trajetória individual do cão como preditor da trajetória individual do bêbado, os resultados seriam potencialmente espúrios. O que fazer então para estimar modelos com séries não estacionárias?
A solução mais simples para esse problema seria identificar a ordem de integração das séries – as trajetórias do bêbado e do cão são integradas de ordem 1 – e estimar o modelo de interesse com as séries diferenciadas estacionárias – nesse exemplo, usando os passos do cão como preditores dos passos do bêbado. Todavia, ao fazer isso nós desprezamos as possíveis relações de longo prazo entre as séries, já que usamos as variáveis na forma de variação (de curto prazo).
Por outro lado, quando utilizamos as séries integradas e o respectivo vetor de cointegração, a especificação do modelo acaba sendo muito mais rica, permitindo identificar relações de longo prazo, tendências comuns, e efeitos de feedback, por exemplo. Modelos desse tipo, conhecidos como Cointegrated VAR1 ou VEC2, são até hoje uns dos mais usados por economistas e econometristas, pois permitem combinar informação de longo e curto prazo nos dados a partir da propriedade de cointegração.
A anedota do bêbado e seu cachorro é uma boa ilustração dos conceitos de cointegração e correção de erro, e mostra que, ao contrário de outras definições econométricas, cointegração não é meramente uma conveniência estatística, mas sim uma propriedade das séries com conteúdo comportamental relevante! É verdade que a teoria econômica não nos ajuda a prever os passos aleatórios do cão e de seu dono (comportamento de curto prazo entre as variáveis), mas traz importantes insights sobre a relação de longo prazo entre as duas trajetórias.
A ideia de cointegração, apesar de ser mais disseminada na macroeconomia, pode ser usada no mercado financeiro para identificar relações de dependência entre ativos e operar (lucrativamente) em cima disso. De fato, “tentar modelar relações complexas de interdependência entre ativos financeiros apenas com o conceito de correlação é como tentar surfar na internet com um IBM AT”3 (Carol Alexander). A relação de cointegração descreve a distância entre dois ativos ao longo do tempo, enquanto a correlação simples descreve apenas a tendência de movimento em direções semelhantes.
Uma aplicação importante de cointegração em finanças são as estratégias de pairs trading. Nesse tipo de estratégia, uma posição comprada é “pareada” com uma posição vendida de duas ações fortemente correlacionadas (cointegradas). Com isso é possível estabelecer uma posição market neutral, ou seja, que gera retorno independentemente das condições de mercado contanto que a posição comprada suba mais que a posição vendida ou que a posição vendida caia mais do que a posição comprada. Suponha uma estratégia em que os dois ativos pareados são o cão e o bêbado. Uma estratégia de pairs trading aposta que no longo prazo o as trajetórias do cão e do bêbado vão convergir e, portanto, opera exatamente o vetor de cointegração entre eles [1,-1].
Duas ações de um mesmo setor ou duas ações de competidores diretos são altamente correlacionadas (cointegradas) e, portanto, fortes candidatos para pairs trading. Um exemplo de pares seria Vale e CSN Mineração, ambas do setor de mineração. Suponha que você deseje montar uma estratégia pares com VALE3 e CSNA3 e que você tenha certeza que a Vale vai performar melhor do que a CSN. A partir disso, você poderia montar uma posição market neutral comprando Vale e vendendo CSN (com pesos iguais). Mesmo que as duas ações caíssem, contanto que CSNA3 caia mais que VALE3, esse será um negócio lucrativo.
No geral, existem dois tipos pairs trading: um baseado em arbitragem estatística (long/short) e o outro em valuations fundamentalistas (compra ativos baratos e vende ativos caros). No caso de estratégias fundamentalistas, geralmente os ativos são pareados de forma que a ponta long tenha o mesmo número de ativos por setor que a ponta short. Já no caso de estratégias de arbitragem estatística, encontrar os pares de ativos é um desafio por si só.
Você já sabe que fundos quantitativos usam algoritmos e que, por isso, ganham escala na análise de dados, sendo capazes analisar um conjunto de ativos muito maior do que os fundos discricionários tradicionais, por exemplo. Nesse sentido, os quants acabam tendo uma vantagem na hora de identificar potenciais pares de ativos e conseguem implementar estratégias baseadas em arbitragem estatística mais eficientes.
1: Os modelos do tipo VAR (Vector Autorregressive) são o análogo vetorial/multivariado dos modelos autorregressivos (AR).
2: Os modelos do tipo VEC (Vector Error Correction) são o análogo vetorial/multivariado dos modelos de correção de erro (ECM) e podem ser entendidos como modelos do tipo VAR cointegrados.
3: “O IBM Personal Computer/AT (IBM 5170), mais conhecido como IBM AT e também chamado às vezes de PC AT ou PC/AT, foi o computador de segunda geração da IBM, construído com o microprocessador 80286 da Intel a funcionar a 6 MHz (8 Mhz em versões posteriores) e foi posto à venda em 1984 e descontinuado em 1987 por causa do lançamento dos computadores IBM PS/2.” (fonte Wikipedia).
Leia também o texto “Qual a relação entre algoritmos e fundo quant?”
