Um texto sobre como fenômenos complexos podem parecer simples, na vida e no mercado.

Por Gabriel Koike

Quando observamos o mundo através da nossa perspectiva humana, percebemos alguns fenômenos muito complexos por algumas lentes muito limitadas – seja em termos de espaço, tempo, frequências, amplitudes, dimensões ou estados. Entre alguns exemplos dessas limitações da nossa percepção estão a evolução das espécies através da seleção natural, mudanças climáticas globais causadas por ação humana, consciência da mente e preços de mercado. Todos esses exemplos são de fenômenos onde nossa percepção nos ilude – às vezes até fazendo o complexo parecer simples, quando na verdade são fenômenos inerentemente complexos. Sua complexidade surge de interações entre elementos – que muitas vezes seguem regras muito simples – mas que quando levadas em conta de forma sistêmica fazem o comportamento do todo ser muito mais complexo do que a soma das suas partes. Chamamos essa propriedade de emergência – complexidade emergente.

Para enxergar como isso acontece, podemos olhar alguns exemplos. Um dos exemplos mais clássicos e elegantes é o Jogo da Vida de Conway (Conway’s Game of Life). Este é um conjunto de sistemas modelados como autômatos celulares onde elementos seguem regras iguais, claras e bem conhecidas, mas que geram uma série de comportamentos emergentes quando observados como um todo – causando a impressão de que os elementos estão vivos.

O Jogo da Vida de Conway começa com uma série de elementos quadriculados – como posições em um tabuleiro de xadrez – que podem assumir dois estados: vivo ou morto. Definimos também um conjunto de regras bastante simples sobre a evolução dos sistemas a partir dos elementos. Para cada passo de tempo, olhamos o estado anterior e computamos o que acontece:

1. Se um elemento está vivo, mas cercado de menos de dois vizinhos vivos, ele morre. (Regra de escassez)
2. Se um elemento está vivo, cercado de dois a três vizinhos vivos, ele permanece vivo. (Regra de permanência)
3. Se um elemento está vivo, mas cercado de mais de três vizinhos vivos, ele morre. (Regra de sobre-população)
4. Se um elemento está morto, cercado de exatos três vizinhos vivos, ele nasce. (Regra de reprodução)

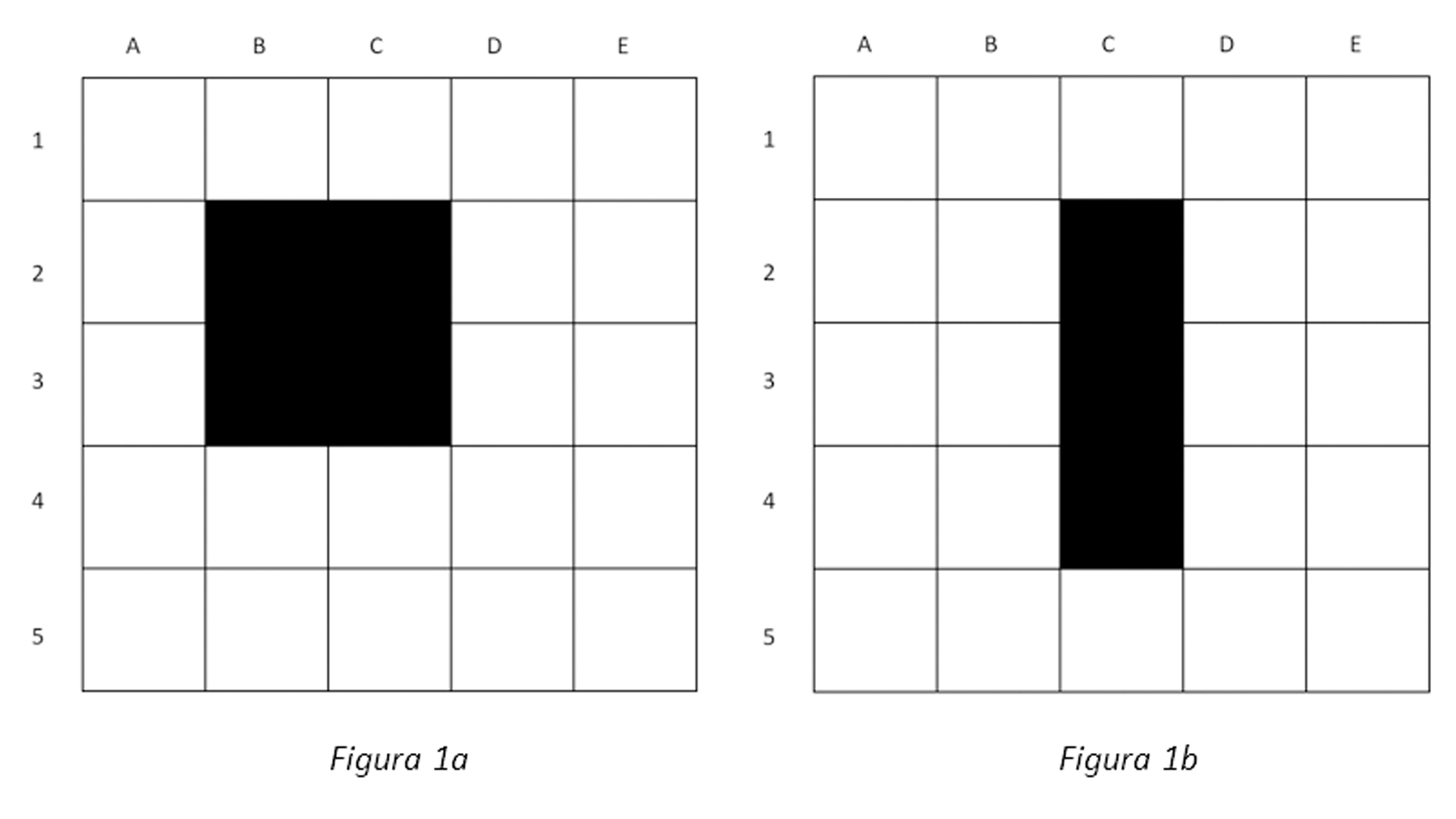
Para ilustrarmos, precisamos de condições iniciais de elementos vivos (preto) ou mortos (branco). Vamos supor olhar dois cenários simples, nas Figuras 1a e 1b.

A figura 1a é bastante simples: cada um dos elementos 2B, 2C, 3B e 3C, cada um, é vizinho de exatamente 3 elementos vivos. Portanto, esperamos que cada um deles permaneça vivo na próxima iteração. Da mesma forma, elementos ao redor que estão mortos não estão cercados de 3 vizinhos vivos e, portanto, permanecem mortos. A figura 1b é um pouco mais interessante. Notamos que os elementos 3B e 3D estão mortos, mas cercados de 3 elementos vivos (2C, 3C e 4C). Portanto, na próxima iteração estarão vivos. Os elementos 2C e 4C, por sua vez, mas são vizinhos apenas de 3C vivo. Nesse caso, estarão mortos na próxima iteração. E o elemento 3C, vivo, é vizinho de dois elementos vivos e, portanto, permanece vivo na próxima iteração. A segunda iteração, portanto, é mostrada na figura 2a e 2b.

Notamos que a figura 2a é idêntica à figura 1a. Este conjunto é estável, e não muda não importa quanto tempo passe. Já a figura 2b é um pouco diferente, mas semelhante a 1b – uma translação. Evidentemente na próxima iteração, os elementos da figura 2b formarão exatamente o mesmo padrão de 1b. Nesse caso, temos um oscilador de período 2.

Estes exemplos são bastante simples. Mas existem padrões muito mais complexos. Osciladores de períodos maiores, padrões “que andam”, padrões que geram outros padrões, entre outros. Na verdade, a complexidade deste sistema é incrível, e gerada a partir de apenas regras simples. A figura 3 é uma ilustração da complexidade deste sistema, em uma simulação.

Na verdade, este sistema é tão complexo que é chamado, na Teoria de Complexidade Computacional, de indecidível (undecidable) – é impossível a construção de um algoritmo que possa determinar de forma definitiva a posição final ou se o sistema é “infinito”, dada qualquer posição inicial. Este sistema se enquadra em uma classe de regras chamada Turing-Completa (Turing Complete) e isso é o análogo do Problema de Parada (Halting Problem).

O Jogo da Vida de Conway é fascinante, e dele tiramos alguns conceitos muito importantes para nosso mundo de matemática, modelagem e simulação:

1. A interação de diversos elementos, mesmo que seguindo regras simples, pode dar origem a fenômenos complexos em um “nível macro”.
2. Alguns fenômenos aparentemente imprevisíveis são apenas consequência de diversos elementos que interagem entre si com o tempo, mesmo que seguindo regras simples – ou podem ser modelados como tal.
3. Pequenas variações em condições iniciais de alguns sistemas podem gerar grandes diferenças, e aparentemente imprevisíveis, na evolução destes. Isto é uma propriedade, inclusive, de Sistemas Caóticos – apesar de não suficiente.

No primeiro parágrafo, citamos alguns exemplos de fenômenos emergentes – sob a ótica de nossa limitação em enxergar apenas algumas propriedades “macro” de forma intuitiva. Podemos ver como cada um deles se relaciona com estes conceitos.

Tanto a evolução das espécies através da seleção natural quanto mudanças climáticas são difíceis para nossa percepção porque nossas limitações de observação são limitadas a nossos dias, meses e anos, enquanto precisaríamos de centenas, milhares ou milhões de anos (no caso da evolução) para notar alguns destes efeitos. No entanto, sabemos de regras simples que elementos que compõem estes sistemas seguem – o clima pode ser modelado como pequenas células que seguem regras de temperaturas, pressões, humidade, composição de gases, troca de calor e composição atmosférica, e diversos fenômenos físicos.

Já a evolução de espécies por seleção natural foi desmistificada com a evolução da genética e validada com uma série de predições que a teoria faz. Em ambos os casos, o uso de modelagem e simulações pode ajudar a elucidar alguns conceitos e refinar o entendimento teórico. Já o pensamento e consciência humanas são fenômenos emergentes da interação de neurônios conectados através de sinapses, diversidade de dendritos, células especializadas, camadas de neurônios, regiões funcionais de células e a interação entre as diversas regiões.

Em todos estes exemplos, ainda há muito a ser refinado – mas o conhecimento científico sobre estes temas progrediu muito com a compreensão de complexidade como fenômenos emergentes, além do uso extensivo de modelos matemáticos e simulações.

Por fim, mencionamos preços de mercado. Voltamos então ao nosso artigo de Microestruturas de Mercado. Com microestruturas de mercado, passamos a ver preços como consequências de interações entre compradores e vendedores, cada um com preços a que aceitam negociar ativos. Refraseando como o tema deste artigo: os preços de mercado também podem ser vistos (e modelados) como fenômenos emergentes, partindo-se de diversos elementos que negociam ativos. Cada elemento do sistema pode possuir um nível de informação (ou conhecimento) diferente, e busca maximizar seu retorno de acordo com seus critérios e limitações financeiras.

Compradores buscam comprar ativos ao menor preço possível. Se um comprador tem acesso a alguma informação que o leve a aceitar um preço a que um vendedor está disposto a vender, ocorre um negócio (trade). Da mesma forma, se um vendedor tem acesso a informação suficiente que o leve a aceitar vender pelo preço mais alto que está sendo pedido por compradores, ocorre um negócio. E assim, os preços de negócios se formam.

O sistema de compras e vendas é um leilão duplo – com preços de oferta e demanda (bid e ask). Há diversos participantes, mas nem todos os participantes são iguais. Existem modelos onde os participantes são diferenciados entre informados e não informados (informed trading vs uninformed trading). Além disso, participantes podem ter acessos aos preços com maior ou menor atraso. Por fim é bastante pertinente citar que há algoritmos que operam em mercados de forma razoavelmente previsível – como por exemplo um participante que execute grandes ordens de alguns ativos (como, por exemplo, durante um rebalanceamento de um índice de mercado) usando um algoritmo do tipo VWAP (Volume Weighted Average Price) ou TWAP (Time Weighted Average Price), ordens de stop automático ou mesmo grandes participantes fazendo operações de delta hedge.

Enquanto tudo isso acontece, os preços de negócios oscilam de forma imprevisível. Mesmo que todos os inúmeros participantes de mercado tivessem seus parâmetros perfeitamente conhecidos – preferências, preços que aceitam compras ou vendas, nível de informação, atrasos etc. – os preços formados pela interação destes poderia ser incrivelmente complexa, e muito provavelmente um problema indecidível (como uma Máquina de Turing). Certamente com variações de parâmetros, os preços serão imprevisíveis. E ao mesmo tempo, alguns participantes de mercado buscam padrões geométricos em gráficos formados por estes preços para tomar as suas próprias decisões, na vida real.

Modelos econométricos em geral representam retornos de mercado como séries temporais sequenciais de variáveis aleatórias, com diversos níveis de sofisticação e com diferentes propriedades matemáticas, apesar de buscarem representar um conjunto semelhante de fatos estilizados. Boa parte dos modelos de retornos de mercado são tais que preços são Martingales (sequências de variáveis aleatórias tais que a expectativa condicional do próximo preço é o próprio preço anterior) ou representam ativos como regressões lineares (ou até regressões mais sofisticadas), com relação a um índice de mercado ou mesmo a outros ativos – como mostramos no nosso artigo de Cointegração.

Modelos de microestrutura e representações de elementos simples interagindo em uma rede complexa, tais que preços ou retornos surgem como fenômenos emergentes, também podem dar origem a preços e retornos que se comportam de formas semelhantes a modelos econométricos. Inclusive, é possível observar quais premissas sobre os elementos são necessárias para dar origens a Martingales, a ativos correlacionados ou a outros tipos de fenômenos. E um dos grandes valores desse tipo de conhecimento é entender as limitações ou as condições que precisam ser satisfeitas (como limitações sobre liquidez, atrasos, assimetria de informação) para que alguns modelos econométricos sejam boas representações.

Complexidade como um fenômeno emergente é um tema fascinante. Sob o ponto de vista matemático, é incrível ver como elementos simples podem interagir de forma a gerar comportamentos tão complexos e ricos. Esta forma “bottom-up” de ver alguns fenômenos é uma ferramenta poderosíssima, que nos permite desenvolver ou refinar teorias, ver similaridades e analogias entre diferentes áreas do conhecimento. É mais uma ferramenta que devemos ter em nosso repertório. Esta ferramenta requer grande capacidade de análise e simulação, mas ao mesmo tempo ilumina nosso entendimento de nossos modelos e confiança nestes, com uma capacidade não atingida quando olhamos o mundo “top-down”.

Leia também o texto “Tempo, Natal, e Microestruturas de Mercado”.